Reiten Sie die Welle(n) und werden Sie EXCITEd

Die Motivation für die ganze Geschichte ist eine Technik namens Zeit-Frequenz-Analyse, die aus der Signalverarbeitung stammt. In einfachen Worten: Sie liefert den Frequenzinhalt eines Signals (oder eines Simulationsergebnisses) das als Zeitreihe vorliegt.

AVL EXCITE™ M ist bekannt und geschätzt für seine herausragenden Fähigkeiten zur Lösung von dynamischen Bewegungen flexibler Körper und ihrer gegenseitigen Kontakte (z.B. bei Lagern, Zahnrädern, Kolben) im Zeitbereich. Dies ist eine großartige Methode, um hochgradig nichtlineares Verhalten darzustellen und die vollständige Interaktion zwischen Körperbewegung und Kontakten darzustellen. NVH-Ingenieure – und Menschen im Allgemeinen – neigen jedoch dazu, Lärm und Vibrationen in Form von Frequenzen wahrzunehmen. Folglich brauchen wir etwas, um vom Zeit- in den Frequenzbereich zu konvertieren.

Glücklicherweise gibt es bereits ein umfangreiches Instrumentarium. Lassen Sie uns einige nützliche Instrumente vorstellen, die uns zur Verfügung stehen.

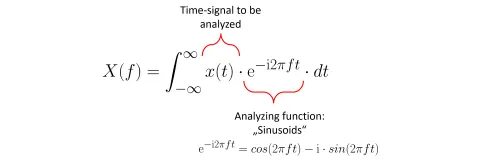
Dies ist die einfachste Methode, um ein Zeitsignal x(t) in den Frequenzbereich X(f) zu übertragen. Die Idee ist einfach, dass man entlang der Frequenzen f (von -∞ bis +∞ ) wandert und eine „Sinuskurve“ dieser Frequenz als Analysefunktion verwendet. Durch Multiplikation (genauer genommen ein Skalarprodukt) des zu analysierenden Signals mit der „Prüfsinuskurve“ erhält man die Amplitude und den Phasenwinkel bei einer bestimmten Frequenz. Dies ist eigentlich ein recht einfacher und intuitiver Prozess.

Für formelsüchtige Leser kann dies wie in Abbildung 1 dargestellt werden. Für Leser, die sich vor Formeln ekeln, bleibt es bei der gedanklichen Vorstellung der Projektion auf die Analysesinuskurven.

Bei näherer Betrachtung dieses Konzepts wird deutlich, dass es nur dann zuverlässig funktioniert, wenn wir ein stationäres und periodisches Signal haben. Andernfalls ergibt die Multiplikation mit den analysierenden Sinusschwingungen Zufallszahlen und die Ergebnisse sind schlichtweg Quatsch. In netteren Worten: Das bedeutet, dass die FT nicht in der Lage ist, lokalisierte Frequenzinhalte so wiederzugeben, wie sie etwa bei einem Stoßvorgang oder anderen instationären Prozess entstehen.

Aber halt! Was ist zu tun, wenn ein transientes Signal zu untersuchen ist? Keine Panik, bleiben Sie ruhig! Die Antwort auf diese heikle Frage finden Sie im nächsten Abschnitt. Hören Sie also nicht auf, hier zu lesen, sonst verpassen Sie den entscheidenden Punkt!

Bevor wir fortfahren, noch eine kleine Ergänzung: Die Fourier-Transformation und ihr schnellerer Bruder, die so genannte Fast Fourier Transform (FFT), steht EXCITE M-Anwendern über AVL IMPRESS™ M und excitePost zur Verfügung.

Viele der Signale, mit denen wir zu tun haben, variieren in der Zeit, was eine sogenannte Zeit-Frequenz-Analyse erfordert. Die klassische Methode, die dafür verwendet wird, ist die Kurzzeit-Fourier-Transformation (STFT).

Der Clou dieser Methode ist: Eine konstante Fensterfunktion – ähnlich dem in der FT verwendeten Hann-Fenster – wird auf einen kleinen Zeitabschnitt des Signals angewandt, wo dann die Fourier-Transformation berechnet wird.

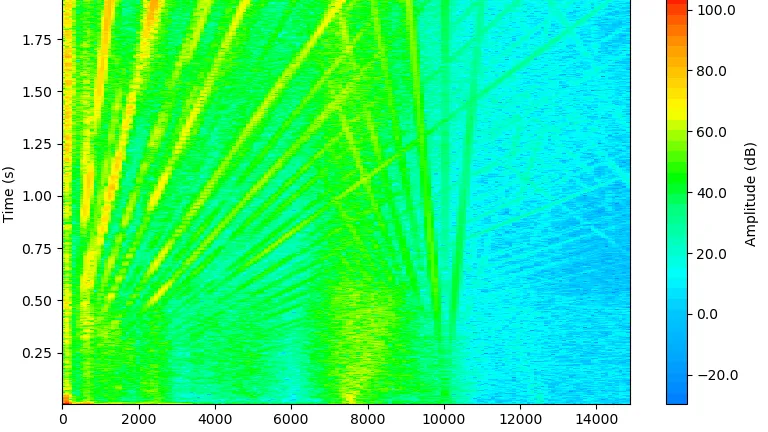
Führt man dies für jeden Zeitschritt durch und fügt sie alle zusammen (unter Verwendung einer sog. Faltung), so erhält man eine gültige Fourier-Transformation für das nichtstationäre Signal, deren Darstellung als Spektrogramm bezeichnet wird (Abbildung 2).

(Beachten Sie, dass verschiedene Versionen von Spektrogrammen üblich sind, eine mit der Zeitachse auf der Abszisse, eine mit der Zeitachse als Ordinate).

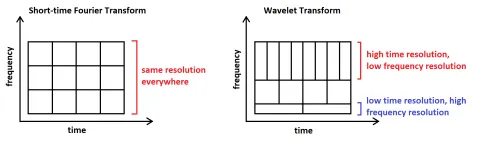
All dies sieht so weit gut aus, aber es gibt trotzdem einen großen Nachteil bei der STFT, und zwar den Kompromiss zwischen Zeitauflösung und Frequenzauflösung. Dies wird als Gabor-Unschärfe bezeichnet und ist mit der Heisenberg-Unschärfe in der Quantenmechanik vergleichbar. Die folgende Abbildung 3 stellt diese Unsicherheit visuell dar und zeigt das Minimum in Form eines Flächenelements der Diskretisierung des Spektrogramms, das wir als „Kacheln“ bezeichnen.

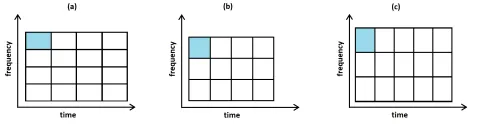
Für unser Spektrogramm bedeutet dies, dass wir entweder eine hohe Zeitauflösung oder eine hohe Frequenzauflösung haben können, aber nicht beides gleichzeitig. Diese Unsicherheit lässt sich nicht vermeiden und ist besonders bei Signalen mit einem sehr großen Frequenzbereich störend.

Dieses Problem lässt sich gut am folgenden Beispiel veranschaulichen: Wir werden eine STFT an einem hyperbolischen Chirp-Signal durchführen, das in SciPy erzeugt wurde. Der Chirp hat die folgenden Parameter:

Start: Zeit t = 0,0 s, Frequenz f = 1500 Hz

Ende: Zeit t = 2,0 s, Frequenz f = 50 Hz

Schauen wir uns an, wie gut das Spektrogramm diese Parameter wiedergibt (Abbildung 4).

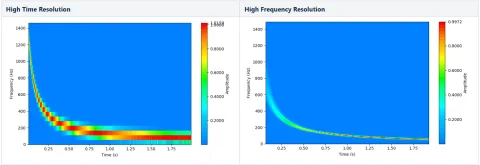
Keines dieser Spektrogramme ist optimal für die Darstellung unseres Signals. Die hohe Zeitauflösung ergibt eine genauere Darstellung des hyperbolischen Chirps gegen t = 0 (mit f = 1500 Hz), ist aber auf der Frequenzachse sichtbar „abgehackt“, was besonders bei den niedrigen Frequenzen problematisch ist.

Die Hochfrequenzauflösung ist durchweg glatter, aber das Signal kommt nicht einmal in die Nähe der Anfangsfrequenz von 1500 Hz (weil der Zeitpunkt, zu dem es diese Frequenz erreichen sollte, im Spektrogramm nicht korrekt angezeigt wird!). Auch im linken Bild erreicht das Signal nicht ganz die 1500 Hz, aber wenn die Abtastung so gewählt worden wäre, dass sie es erreicht, wäre das Spektrogramm auf der Frequenzachse völlig unleserlich gewesen. Dies stellt ein erhebliches Problem dar, wenn der Frequenzbereich des Signals groß ist und wir Einschwingvorgänge und Ordnungen ablesen möchten, wie z. B. bei einem Motorhochlauf.

Glücklicherweise gibt es eine Möglichkeit, dieses Problem zu umgehen, indem man die Auflösung für bestimmte Teile des Spektrogramms priorisiert; hier kommen die Wavelets ins Spiel.

Zur Einstimmung auf die WT sprechen wir zunächst über deren Auflösungsbesonderheiten. Typischerweise ändern sich niederfrequente Komponenten langsam im Laufe der Zeit, so dass hier keine hohe Zeitauflösung erforderlich ist, aber wir brauchen eine hohe Frequenzauflösung. Hohe Frequenzen treten über kürzere Zeiträume auf, so dass die Zeitauflösung hier eine Rolle spielt, aber unsere Frequenzauflösung muss nicht so hoch sein.

Man sieht, dass es sinnvoll ist, die Kachelung des Spektrogramms zu ändern, um die richtige Auflösung in den wichtigen Bereichen zu erreichen. Die Art und Weise, wie dies bei der Wavelet-Transformation geschieht, wird im Folgenden dargestellt (Abbildung 5):

Wenden wir nun die Wavelet-Transformation auf unseren hyperbolischen Chirp von oben an (Abbildung 6):

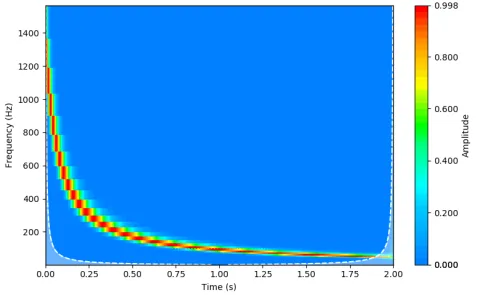
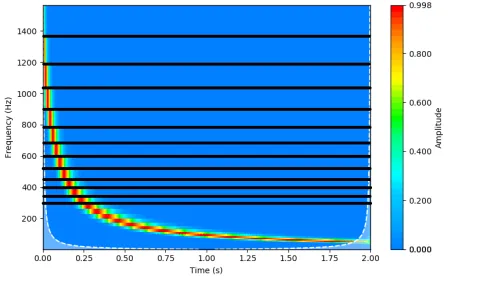
Bei einer linearen Frequenzskala ist die Kachelung leicht zu erkennen, und wir haben eine Darstellung unseres Signals, die sowohl bei der Ausgangsfrequenz von 1500 Hz exakt ist als auch auf der Frequenzachse sinnvoll abgetastet wurde.

Nachdem Sie die Ausgabe gesehen haben, fragen Sie sich vielleicht: Was macht die Wavelet-Transformation? Ist sie nur ein schickes STFT-Fenster mit verschiedenen Kacheln? Um die zweite Frage zu beantworten: Technisch gesehen, ja. Beide Methoden verwenden eine Faltung, um eine Fensterfunktion über das Signal zu schieben, und hängen von einer Zeitverschiebung und einem Frequenzparameter ab, was zu einem Vektor von Koeffizienten führt, welcher die Amplitude des Signals zu jedem Zeitpunkt bei der gegebenen Frequenz darstellen. Wenn man sich jedoch auf der Frequenzachse nach oben bewegt (siehe die Kacheln), ändert sich die Größe des Wavelets. Zu Beginn ist es zeitlich breit und frequenzmäßig schmal, um die kleineren Frequenzen zu erfassen, und es wird zeitlich schmaler und frequenzmäßig breiter, um kleinere Zeitabschnitte zu betrachten.

Daraus ergibt sich eine logarithmische „Skalierungsachse“. Man sollte mit dem Wort „Frequenzachse“ vorsichtig sein, da die Skalierung nicht gleich, sondern nur proportional zur Frequenz ist. Sie müssen unter Verwendung der Abtastzeit in Frequenzen umgewandelt werden, um nützliche Informationen aus der Darstellung zu erhalten. Die Darstellung wird als Skalogramm und nicht als Spektrogramm bezeichnet.

Nun der grundlegendsten Punkt der WT: Die Fensterfunktion

Während die Kacheln ein wichtiger Aspekt der Wavelet-Analyse sind, sind unsere neuen Fensterfunktionen, die Wavelets selbst, der auffälligste Aspekt.

Wie sieht ein Wavelet aus? Nun, so ziemlich jede Funktion kann als Wavelet dienen, wenn man einige Einschränkungen beachtet. Abbildung 7 zeigt einige der verschiedenen Formen, die ein Wavelet annehmen kann:

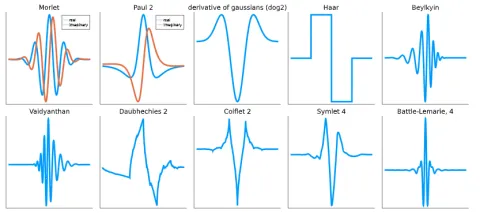
Die Haupteigenschaft, die sie (neben der endlichen Amplitude) gemeinsam haben, ist die Lokalisierung. Dies ist keineswegs überraschend, denn die Alternative, eine Sinusfunktion, die sich über den gesamten Bereich wiederholt, würde lediglich zu einer normalen Fourier-Transformation führen.

Abgesehen davon kann man ein Wavelet nach Belieben gestalten, wobei bestimmte mathematische Eigenschaften je nach Zweck des Wavelets von Vorteil sind.

Wenn Sie sich die 2. Zeile von Abbildung 8 ansehen, werden Sie vielleicht denken: Ok, aber einige der Wavelets sehen eher wie die Kritzeleien eines Kleinkindes aus. Das stimmt, aber wir können Ihnen versichern, dass sie gut konzipiert sind und bestimmten Anforderungen gerecht werden. Zum Beispiel spielen die Daubechies-Wavelets in der Klimaforschung eine wichtige Rolle, weil sie das Signal-Rausch-Verhältnis von Gaskonzentrationsmessungen erheblich verbessern.

Die Wavelet-Transformation, wie sie in der Zeit-Frequenz-Analyse COMPOSE App angewendet wird:

Mit der Version 2024 R1 bietet die COMPOSE App Zeit-Frequenz-Analyse neben der STFT auch Wavelets an. Sie kann über die EXCITE M App-Library aufgerufen werden und ist über das Hauptmenüband zugänglich (Abbildung 9).

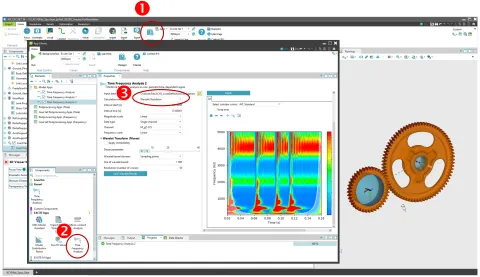
In der COMPOSE-App „Zeit-Frequenz-Analyse“ wurde das „Morse-Wavelet“ implementiert, das eine so genannte „Familie“ darstellt, da seine Form parameterabhängig ist (Abbildung 9). Dies ermöglicht dem Benutzer eine größere Vielseitigkeit, da die Parameter für die ideale Wavelet-Form angepasst werden können.

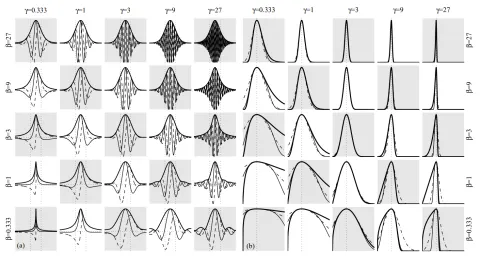
Die „ideale Wavelet-Form“ klingt ein wenig willkürlich, und das ist sie auch. Sie hängt hauptsächlich von zwei Faktoren ab: Der Priorität des Benutzers für die Auflösung (Zeit oder Frequenz) und der Form des Signals. Beginnen wir mit dem konkreteren Faktor: Die Auflösungspriorität.

Trotz der Bemühungen, die mathematischen Details und die Theorie in diesem Text nicht zu sehr in den Vordergrund zu rücken, hat der Leser vielleicht schon bemerkt, dass eine beträchtliche Menge von beidem in die Durchführung der Wavelet-Analyse fließt. Um die Anwendung so benutzerfreundlich wie möglich zu halten, sind ein paar Vereinfachungen notwendig.

Die obige Abbildung, die alle möglichen Morse-Wavelet-Formen zeigt, die von zwei Parametern abhängen, ist zwar schön und gut, aber diese beiden Parameter haben ähnliche Auswirkungen auf das Skalogramm (Zeit-/Frequenzauflösung).

Daher ist in der COMPOSE App der Parameter g festgelegt und nur der Parameter β bleibt der Benutzereingabe überlassen.

Abbildung 10 zeigt die Auswirkung des Parameters β auf ein künstliches Impulssignal, das zur besseren Veranschaulichung der Unterschiede in logarithmischen Frequenz- und Amplitudenskalen dargestellt ist.

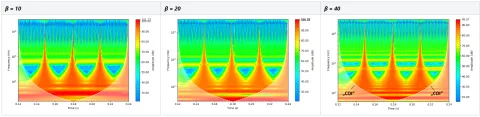
Der Kompromiss zwischen Zeit und Frequenz ist hier deutlich sichtbar. Je kleiner der Parameter β ist, desto höher ist die Zeitauflösung. Je größer β ist, desto höher ist die Frequenzauflösung. Während die Parametereingabe in Form eines Schiebereglers erfolgt und nahezu stufenlos variiert werden kann, empfiehlt die App fixierte Werte, welche verschiedene bekannte Wavelets approximieren:

• Morlet-Wavelet: Höhere Zeitauflösung
• Bump-Wavelet: Höhere Frequenzauflösung

Der zweite Faktor, den es bei der Wahl des β-Parameters zu beachten gilt, ist die Form des Signals. Hier kommt der eher willkürliche Teil ins Spiel: Als Faustregel gilt, dass ein Wavelet verwendet werden sollte, das eine ähnliche Form wie das Originalsignal hat. Bei der Vielzahl der existierenden Signale ist dies etwas schwierig zu überprüfen. Daher empfiehlt es sich für den Benutzer, einige Parameter auszuprobieren. Die Antwort auf die Frage, ob dies ein Vorteil oder ein Nachteil ist, hängt davon ab, wie abenteuerlustig der Benutzer ist.

Eine Besonderheit der Wavelet-Analyse ist der so genannte „Cone of influence“ (COI) (siehe Abbildung 11, rechts). Dabei handelt es sich um das mysteriöse Merkmal, das wir in unserer Einleitung erwähnt haben. Er ist am Anfang und am Ende der Zeitachse des Skalogramms sichtbar. Die COI erscheint aufgrund des Unterschieds zwischen der Signalgröße und der Wavelet-Größe, der mit der Faltung nicht vereinbar ist. Daher muss das Signal am Anfang und am Ende mit Nullen aufgefüllt werden, was zu einer Unterbrechung der Periodizität in diesen Bereichen und damit zu Artefakten führt. Die COI trennt den üblichen Bereich, in dem die Artefakte auftreten, vom Rest des Signals, und der Benutzer sollte sich bewusst sein, dass der Bereich außerhalb der COI mit Vorsicht behandelt werden sollte.

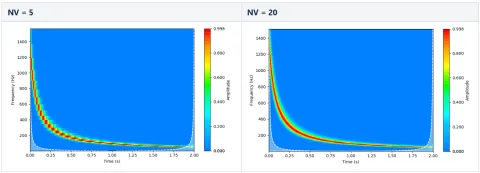
Der letzte Eingabeparameter ist die „Anzahl der Stimmen“ (NV), wobei der Benutzer die Anzahl der Schritte zwischen zwei Oktaven wählen kann. Eine höhere Anzahl von Schritten führt zu einer höheren Frequenzauflösung (bis zur Gabor-Grenze, wie wir wissen) auf Kosten der Rechenzeit, da mehr Koeffizienten entlang der Frequenz-Achse zu berechnen sind. Der Unterschied ist in der folgenden Abbildung 12 zu sehen, in der unser hyperbolischer Chirp von vorhin verwendet wird.

Um Ihr Vertrauen in Wavelets weiter zu stärken, haben wir ein reales Anwendungsbeispiel vorbereitet, nämlich das sog. Hämmern einer Zahnradstufe.

Während das kleine Zahnrad (=Ritzel) mit einer konstanten Drehzahl angetrieben wird, ist das größere Zahnrad einem wechselnden Lastmoment ausgesetzt. Dies führt zu Veränderungen im Flankenkontakt der Verzahnung und erzeugt wiederholte Stöße, wie im Zeitverlauf des Zahnrad-Verbindungsmoments zu sehen ist (Abbildung 13, oben).

Bei Betrachtung des Zeitverlaufs lassen sich für jeden der Stöße die folgenden charakteristischen Bereiche erkennen:

• Der eigentliche Stoß (blaue Sterne), der so intensiv ist, dass zahlreiche Eigenfrequenzen des Systems angeregt werden
• Eine Phase, in der die dominanten Eigenfrequenzen des Systems (bei etwa 400 Hz und 800 Hz) abklingen (1)
• Eine Phase des stationären Zahnradkontakts mit dominierender Eingriffsfrequenz der Verzahnung bei 2050 Hz (=1. Verzahnungsordnung) und 4200 Hz (=2. Verzahnungsordnung) (2)

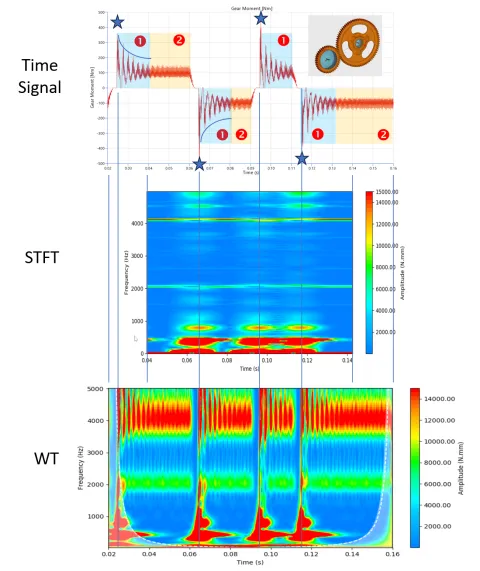
Die STFT (Abbildung 13, Mitte) ist eigentlich nicht schlecht, erfordert aber eine gewisse Abstimmung, um den besten Kompromiss zwischen Zeit- und Frequenzauflösung zu finden. Letztendlich gelingt es ihr jedoch, sowohl die Stöße als auch die Frequenzen des Zahneingriffs in angemessener Weise aufzulösen.

Aber nun sehen Sie sich an, was die Wavelet-Transformation leisten kann! Sie liefert ein großartiges Bild davon, was im System vor sich geht (Abbildung 13, unten). Die Sichtbarkeit der lokalen Details ist einfach erstaunlich. Man kann sogar sehen, dass die Zahneingriffsfrequenzen unterbrochen werden, während die Flanken ihren Kontakt verlieren und durch das Verzahnungsspiel wandern. Auch die periodischen Zahneingriffsstöße entlang der 2050Hz- und 4100 Hz-Linie werden deutlich abgebildet. Gut gemacht, kleine Wavelets!

Schlussfolgerungen

Wenn Sie bis zu diesem Punkt des Artikels vorgedrungen sind, werden Sie festgestellt haben, dass das Konzept der Wavelet-Transformation nichts Geheimnisvolles ist. Ganz im Gegenteil - es ist eine recht intuitive Methode. Wir hoffen, Ihnen den Begriff „Wavelet“ ein wenig näher gebracht zu haben. Die Wavelet-Transformation verwendet das, was der Name schon sagt - kleine Wellen, die Sie in Ihrem Signal verschieben und skalieren und so lokalisierte Frequenzinformationen in ein Diagramm, dem sogenannte Skalogramm, extrahieren. Wir haben diese Funktion in der Zeit-Frequenz-COMPOSE-App angeboten, um die Erstellung von aussagekräftigen Diagrammen mit mehr Details im Vergleich zur Kurzzeit-Fourier-Transformation zu erleichtern. Möge die Wavelet-Transformation mit Ihnen sein, und möge sie Ihnen bei der Verbesserung der Frequenzanalyse Ihrer Simulationsergebnisse gute Dienste leisten.

Referenzen und Quellen

Einen guten Einblick in die Zeit-Frequenz-Analyse gibt Michael X Cohen in seinem Youtube-Kanal: https://www.youtube.com/playlist?list=PLn0OLiymPak2BYu–bR0ADNBJsC4kuRWs
Hier kann man mehr Informationen über das intuitivste Wavelet, das Morlet-Wavelet, finden: Morlet wavelet - Wikipedia
Darüber hinaus bietet auch MATLAB eine Fülle von allgemeinen Informationen in Time-Frequency Analysis and Continuous Wavelet Transform - MATLAB & Simulink - MathWorks Deutschland
Wer sich eingehender mit der Wavelet-Analyse beschäftigen möchte, dem empfehlen wir das Buch „A wavelet tour of signal processing“ von Stéphane Mallat (https://www.sciencedirect.com/book/9780123743701/a-wavelet-tour-of-signal-processing)

Danksagung

Wir möchten unseren besonderen Dank an Franz Diwoky aussprechen, der die Entwicklung dieses Features maßgeblich betreut und unterstützt hat.