EXCITEで乗りこなすウェーブレット信号解析

このストーリー全体の動機となっているのは、時間周波数解析（Time-Frequency Analysis） と呼ばれる技術です。もともとは信号処理の分野から生まれたものです。
簡単に言えば、これは時間信号（あるいはシミュレーション結果）から、その中に含まれる周波数成分を取り出す方法です。

AVL EXCITE™ M は、柔軟体の運動とそれらの相互接触（例：ベアリング、ギヤ、ピストンで発生するもの）を時間領域で解く優れた能力により、広く知られ高く評価されています。
これは、非常に非線形な挙動を再現しつつ、物体運動と接触の完全な相互作用を保持できる優れた手法です。
しかし、NVHエンジニア――そして人間一般も――は、騒音や振動を「周波数」という観点で知覚する傾向があります。したがって、時間領域から周波数領域へ変換するための手段が必要となります。
幸いなことに、すでに豊富なツールボックスが存在します。
ここでは、私たちが利用できる便利な道具をいくつか紹介しましょう。

これは、信号を時間領域 x(t)から周波数領域 X(f)に移すための最も基本的な方法です。
発想は単純で、周波数 fを −∞から +∞まで順に取り、その周波数の「正弦波」を解析関数として用いるというものです。
解析したい信号と、その「調査用の正弦波」とを掛け合わせ（内積を取る）ことで、特定の周波数における振幅と位相角を得ることができます。
実際のところ、これは非常にシンプルで直感的なプロセスです。

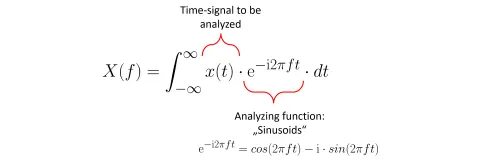
数式好きの読者には、この手法は図1のように数式で表すことができます。
一方、数式嫌いの読者は、「解析用の正弦波への射影」というイメージを頭に描いて読み進めていただければ十分です。

この概念をもう少し掘り下げてみると、フーリエ変換が本当に信頼できる形で機能するのは、信号が定常的かつ周期的である場合に限られることが明らかになります。
そうでない場合、解析用の正弦波との掛け算はランダムな数値を吐き出し、結果は単にデタラメになってしまいます。
もう少し丁寧な言い方をすれば、フーリエ変換は衝撃などから生じる局所的な周波数成分を表現する能力を持たない、ということです。
それでは、解析対象が過渡的な信号である場合はどうすればよいのでしょうか。
その答えは次の段落で解説します。ぜひこのままお読みください。

先に進む前に少し補足です。
フーリエ変換の機能、そしてその高速版である 高速フーリエ変換（FFT） は、AVL IMPRESS™ M および excitePost を通じて EXCITE M のユーザーが利用可能です。

私たちが扱う多くの信号は時間とともに変化するため、いわゆる時間‐周波数解析が必要となります。
この解析で古典的かつ代表的に用いられる手法が、短時間フーリエ変換（STFT） です。
この手法の仕組みはこうです。フーリエ変換（FT）で使われるハン窓に似た一定の窓関数を、信号の短い時間区間に適用し、その区間に対してフーリエ変換を計算します。
これをすべての時間ステップに繰り返して結果をつなぎ合わせ（畳み込みを使って）、非定常信号に対する有効なフーリエ変換を得ることができます。その結果を描いたものがスペクトログラム（図2）と呼ばれるものです。
（なお、スペクトログラムにはいくつかのバリエーションがあり、時間軸を横軸にとるものと、縦軸にとるものの両方がよく使われます。）

ここまでの内容は良さそうに見えますが、STFTには大きな欠点があります。
それは時間分解能と周波数分解能のトレードオフという形で現れます。
これはガボールの不確定性と呼ばれ、量子力学におけるハイゼンベルグの不確定性原理に類似しています。
次の図3は、この不確定性を視覚的に表したもので、スペクトログラムを離散化したときの要素面積として最小値が示されています。
私たちはこれを「タイル（tiling）」と呼ぶことにします。

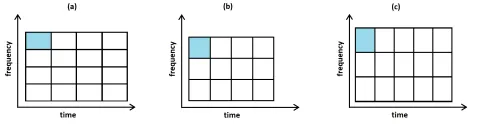
私たちのスペクトログラムにおいては、高い時間分解能か高い周波数分解能のいずれかを選ぶことはできますが、両方を同時に得ることはできません。
この不確定性は避けられず、特に非常に広い周波数帯域を持つ信号に対しては厄介な問題となります。

この問題は、次の例でよく確認できます。
ここでは、SciPyで生成したハイパーボリックチャープ信号に対してSTFTを行います。
チャープ信号のパラメーターは以下のとおりです。

開始条件：時間 t = 0.0 s、周波数 f = 1500 Hz

終了条件：時間 t = 2.0 s、周波数 f = 50 Hz

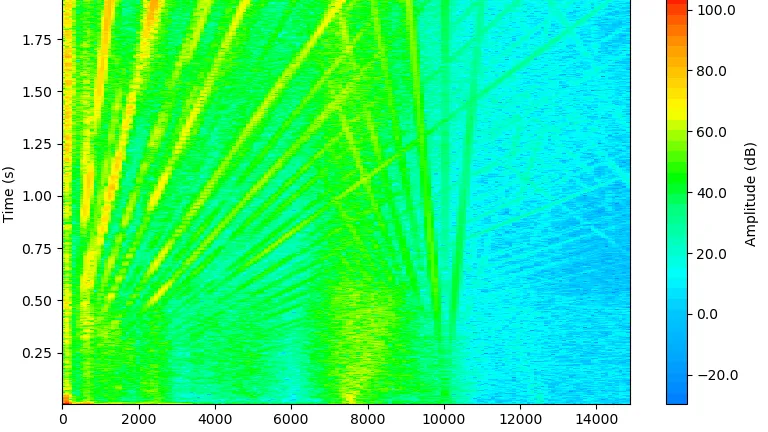
では、スペクトログラムがこれらのパラメーターをどれほどよく表現できているかを見てみましょう（図4）。

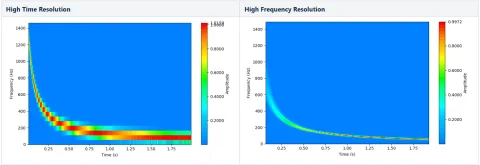
これらのスペクトログラムのどちらも、私たちの信号を表すには最適ではありません。
高い時間分解能のものは、t=0 付近（f=1500 Hz のところ）でのハイパーボリックチャープをより正確に表していますが、周波数軸上では明らかに「ギザギザ」になっており、特に低周波数域で問題となります。
一方、高い周波数分解能のものは全体的に滑らかですが、信号は初期周波数である 1500 Hz にすら到達しません（本来その周波数に達するべき時刻が、スペクトログラム上で正しく表示されていないためです！）。
左側の図においても、信号は完全には 1500 Hz に達していません。しかし、もしサンプリングの設定を変えて到達するようにしたとすると、スペクトログラムは周波数軸上でまったく判読不能になってしまったでしょう。
このことは、信号の周波数範囲が広く、モーターのランアップのように過渡成分や次数を読み取りたい場合に重大な問題となります。

幸いなことに、この問題を回避する方法があります。それは、スペクトログラムの特定の部分に対して分解能を優先させるという発想です。ここで登場するのが「ウェーブレット」です。

WTの詳細な解説に入る前に、まずその分解能の特性について説明します。

一般に、低周波成分は時間的にゆっくりと変化するため、高い時間分解能は必要ありませんが、高い周波数分解能が求められます。
一方、高周波成分は短い時間だけ現れるため、ここでは時間分解能が重要になりますが、周波数分解能をそれほど高くする必要はありません。

重要な領域で適切な分解能を得るためには、スペクトログラムのタイル割りを変更するのが理にかなっていることが分かります。
ウェーブレット変換においては、その方法が次の図（図5）に示されています。

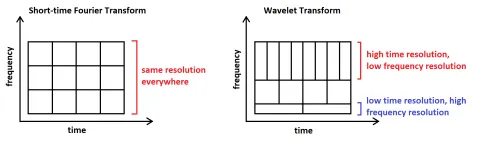
上記のハイパーボリックチャープにウェーブレット変換を適用した結果を図6に示します。

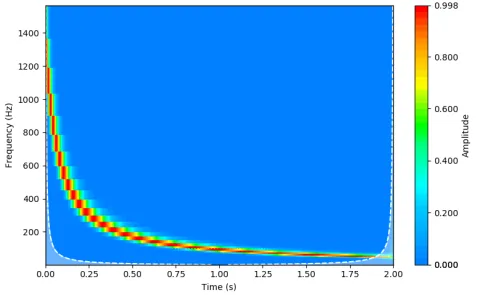
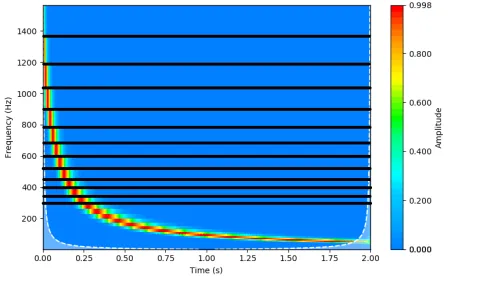
線形の周波数スケールを用いると、タイル割りが容易に確認でき、信号が初期周波数 1500 Hz を正確に表していると同時に、周波数軸上でも適切にサンプリングされていることが分かります。

出力を見たところで、次のような疑問が出てくるかもしれません。
「ウェーブレット変換は何をしているのか？　単にタイル割りの違う高級なSTFTウィンドウなのか？」
この2つ目の問いに答えると――技術的に言えば、その通りです。
両手法とも、窓関数を信号上に畳み込み（コンボリューション）としてスライドさせ、時間方向のシフトと周波数パラメーターに依存しながら処理を行います。その結果、各時刻・各周波数における信号の大きさを表す係数ベクトルが得られます。
ただし、周波数軸を上に移動していくにつれて（タイル割りを参照）、ウェーブレットのサイズは変化します。
低周波数を捉えるときには時間的に広く・周波数的に狭い形から始まり、より高い周波数になると時間的に狭く・周波数的に広い形に変化して、短い時間刻みを観測できるようになります。

これにより、対数的な「スケーリング」軸が得られます。ここで注意すべき点は、「周波数」軸という言葉の使い方です。スケーリングは周波数と等しいのではなく、あくまで比例関係にあるだけです。有用な情報を得るためには、サンプリング時間を用いてスケーリングを周波数に変換する必要があります。このプロットはスペクトログラムではなく、スケログラム（Scalogram）と呼ばれます。

ここで、ウェーブレット変換の最も本質的な要点である「ウィンドウ関数」について説明します。

タイル割りはウェーブレット解析における重要な要素ですが、真に際立っているのは新しいウィンドウ関数、すなわちウェーブレットそのものです。

ウェーブレットはどのような形をしているのでしょうか？――いくつかの制約内であれば、実にさまざまな形をとります。図7には、ウェーブレットが取り得るいくつかの異なる形が示されています。

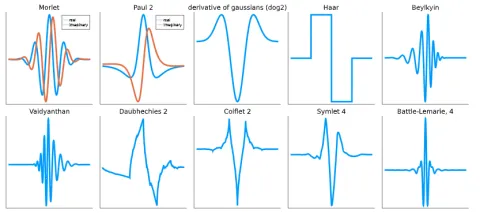
（有限の振幅を持つこと以外で）ウェーブレットに共通する主な特性は、局所性、いわゆる「コンパクトサポート」です。これは全く驚くことではありません。なぜなら、もし波が領域全体で繰り返されるようであれば、それは単なる通常のフーリエ変換になってしまうからです。

それ以外については、用途に応じて有利となるいくつかの数学的性質を考慮しつつ、自由にウェーブレットを設計することができます。
図8の2段目を見ると、こう思うかもしれません。「なるほど、でも中には子どもの落書きみたいに見えるウェーブレットもあるな」と。確かにその通りですが、実際にはそれらはきちんと設計されており、特定のニーズにしっかり応えています。例えば、ドベシー（Daubechies）ウェーブレットは気候研究において重要な役割を果たしており、ガス濃度測定における信号対雑音比（S/N比）を大幅に改善することができます。
 

COMPOSEアプリにおける時間-周波数解析でのウェーブレット変換の適用について。
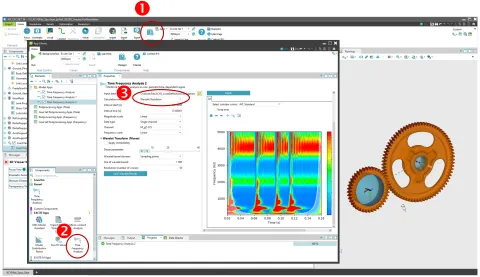
バージョン2024 R1から、COMPOSEアプリの時間-周波数解析ではSTFTに加えてウェーブレットも利用可能になりました。これは EXCITE M アプリライブラリから呼び出すことができ、メインリボンからアクセス可能です（図9）。

時間‐周波数解析 COMPOSEアプリには「モースウェーブレット」が実装されています。これは形状がパラメーターに依存するため「ファミリー」と呼ばれるものです（図10）。この仕組みにより、ユーザーはパラメーターを調整して理想的なウェーブレット形状を選択でき、より柔軟に利用することができます。

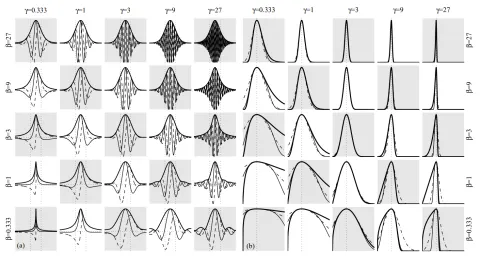
「理想的なウェーブレット形状」というと少し恣意的に聞こえますが、実際その通りです。これは主に2つの要因に依存します。1つはユーザーが重視する分解能（時間か周波数か）、もう1つは信号の形状です。では、より具体的な要因である「分解能の優先度」から見ていきましょう。

数学的な詳細や理論的な部分をできるだけ軽く抑えてきたものの、ここまで読んできた読者は、ウェーブレット解析の実行には相当量のそれらが関わっていることに気づいたかもしれません。アプリをできる限り使いやすく保つためには、いくつかの簡略化が必要となります。
上の図では、2つのパラメーターに依存するモースウェーブレットの全ての可能な形状が示されていますが、これら2つのパラメーターはいずれもスケログラム（時間／周波数分解能）に似たような影響を与えます。
そのため、COMPOSEアプリではパラメーター γ を固定し、ユーザーが入力できるのはパラメーター β のみとしています。

図11は、人工的なインパクト信号に対するパラメーター β の影響を示したものです。違いをより明確に示すため、対数スケールの周波数および振幅で表示されています。

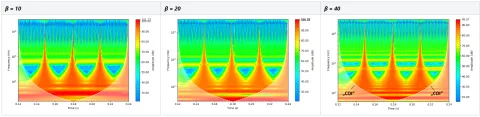
ここでは時間分解能と周波数分解能のトレードオフが明確に見て取れます。パラメーター β が小さいほど時間分解能が高くなり、逆に β が大きいほど周波数分解能が高くなります。パラメーターの入力はスライダー形式でほぼ連続的に変更できますが、アプリでは3つの値が推奨されており、そのうち2つはよく知られた異なるウェーブレットを近似しています。

• モルレーウェーブレット（Morlet wavelet）：時間分解能が高い
• バンプウェーブレット（Bump wavelet）：周波数分解能が高い

βパラメーターを選択する際に考慮すべき2つ目の要因は、信号の形状です。ここに、より恣意的な要素が入ってきます。経験則としては、元の信号と形状が似ているウェーブレットを使用するのが一般的です。しかし、存在する信号の種類は非常に多いため、これを厳密に検証するのはやや困難です。そのため、ユーザーはいくつかのパラメーターを試してみることが推奨されます。これが利点か欠点かは、ユーザーがどれだけ冒険心を持っているかによるでしょう。

ウェーブレットそのもの以外に、ウェーブレット解析において特徴的に現れるのが「影響円錐（Cone of Influence, COI）」と呼ばれるものです（図11右参照）。これは冒頭で触れた“謎のキャラクター”です。スケログラムの時間軸の最初と最後に現れます。COIは、信号の長さとウェーブレットのサイズが一致せず、畳み込みに適合しないことから生じます。そのため、信号の先頭と末尾をゼロで埋める必要があり、この領域では周期性が途切れてアーティファクトが発生します。COIは、アーティファクトが発生する通常の領域とそれ以外の信号部分を分ける役割を持っており、ユーザーはCOIの外側の領域について慎重に取り扱う必要があります。

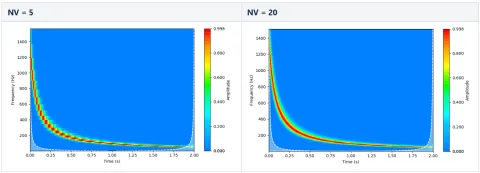
最後の入力パラメーターは「ボイス数（NV: number of voices）」です。これは2つのオクターブ間に設定するステップ数をユーザーが選択できるもので、ステップ数を多くすると周波数分解能が向上します（既に述べたようにガボール限界まで）が、その分、周波数／スケール軸に沿って計算すべき係数が増えるため処理性能は低下します。その違いは、先ほどの双曲線チャープ信号を使った以下の図12で確認できます。

ウェーブレットへの信頼をさらに高めていただくために、実際の応用例をご用意しました。具体的には、単段の歯車ステージにおけるギアハンマリングです。小さなギアは一定速度で駆動される一方、大きなギアには交番負荷トルクが加わります。これにより、かみ合い面の接触が変化し、繰り返し衝撃が発生します。その様子は、歯車接続モーメントのタイムトレース（図13上）に示されています。

• タイムトレースに注目した各衝撃における特徴的領域の識別
• 実際の衝撃（青い星印）── 強く、システムの多数の固有振動数励起
• システムの支配的固有振動数（約400 Hzおよび800 Hz）減衰位相 (1)
• 歯車の定常かみ合い位相── 支配的かみ合い周波数 2050 Hz（1次）および4200 Hz（2次）

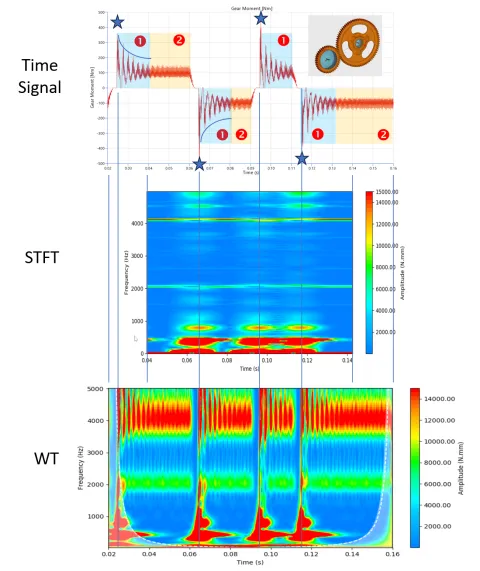
STFT（図13中央）は実際のところ悪くはありませんが、時間分解能と周波数分解能の最適なバランスを見つけるにはかなりの調整が必要です。とはいえ最終的には、衝撃とギアのかみ合い周波数の両方を妥当な形で分離して表現することができます。

では、ウェーブレット変換が何をしてくれるか見てみましょう！　これにより、システム内で起きていることが非常に鮮明に描き出されます（図13下）。局所的な細部の見え方は驚くほど明瞭です。歯のかみ合い面が外れるときに、かみ合い周波数が途切れる様子さえ確認できます。また、2050 Hz と 4100 Hz のラインに沿った周期的なかみ合い衝撃も明確に示されています。

ここまで記事を読み進めていただいた方は、ウェーブレット変換の概念が決して難解なものではないとお気づきになったと思います。むしろ直感的に理解できる手法です。本稿を通じて「ウェーブレット」という言葉に少しでも親しみを持っていただければ幸いです。ウェーブレット変換は、その名の通り「小さな波」を信号全体に平行移動・スケーリングしながら適用することで、局所的な周波数情報を抽出し、スケログラムと呼ばれるプロットとして表現します。

この機能は Time Frequency COMPOSE アプリに実装されており、短時間フーリエ変換（STFT）よりも詳細で意味のあるプロットを容易に作成できるようになっています。ウェーブレット変換が皆様のお役に立ち、シミュレーション結果における周波数成分解析の向上に貢献することを願っています。

参考文献および出典

時間-周波数解析についての優れた洞察は、Michael X Cohen の YouTube チャンネルで得ることができます：Course intro: Understand the Fourier transform and its applications

ここでは、最も直感的なウェーブレットである Morlet ウェーブレット について、さらに詳しい情報を見つけることができます：Morlet wavelet - Wikipedia

さらに、MATLAB も時間-周波数解析および連続ウェーブレット変換に関して豊富な一般情報を提供しています： Time-Frequency Analysis and Continuous Wavelet Transform - MATLAB & Simulink - MathWorks Deutschland

より詳細なウェーブレット解析を求める方には、Stéphane Mallat による著書 『A Wavelet Tour of Signal Processing』 (https://www.sciencedirect.com/book/9780123743701/a-wavelet-tour-of-signal-processing)

を参照することをお勧めします。

謝辞

本機能の開発を力強く監督し、支援してくださった Franz Diwoky氏に、特別な感謝の意を表します。